Quaternion Algebra 2

Quaternion Products

Pure Quaternion Products

\[\begin{aligned} q_a &= [0, \textbf{a}] \\ q_b &= [0, \textbf{b}] \\ q_a \cdot q_b &= [-\textbf{a} \cdot \textbf{b}, \textbf{a} \times \textbf{b}] \end{aligned}\]

Product of Two Unit-Norm Quaternions

Given:

\[\begin{aligned} q_a &= [s_a, \textbf{a}] \\ q_b &= [s_b, \textbf{b}] \end{aligned}\]

And $\vert q_a \vert = \vert q_b \vert = 1$, their product $q_c = q_a \cdot q_b$ is another unit-norm quaternion, where $\vert q_c \vert = 1$

Proof

\[\begin{aligned} q_c = [s_c, \textbf{c}] &= [s_a, \textbf{a}][s_b, \textbf{b}] \\ &= [s_a s_b - \textbf{a} \cdot \textbf{b}, s_a \textbf{b} + s_b \textbf{a} + \textbf{a} \times \textbf{b}] \end{aligned}\]

Assuming the angle between $\textbf{a}$ and $\textbf{b}$ is $\theta$, $s_c = s_a s_b - ab \cos \theta$, while $\textbf{c} = s_a a \hat{\textbf{a}} + s_b b \hat{\textbf{b}} + ab \sin \theta (\hat{\textbf{a}} \times \hat{\textbf{b}})$

\[\begin{aligned} s_c^2 &= (s_a s_b - ab \cos \theta)^2 \\ &= s_a^2 s_b^2 - 2 s_a s_b a b \cos \theta + a^2 b^2 \cos^2 \theta \end{aligned}\]

Now, it is a little bit difficult to find $\textbf{c}^2$, but we can utilize the following diagram to find the answer:

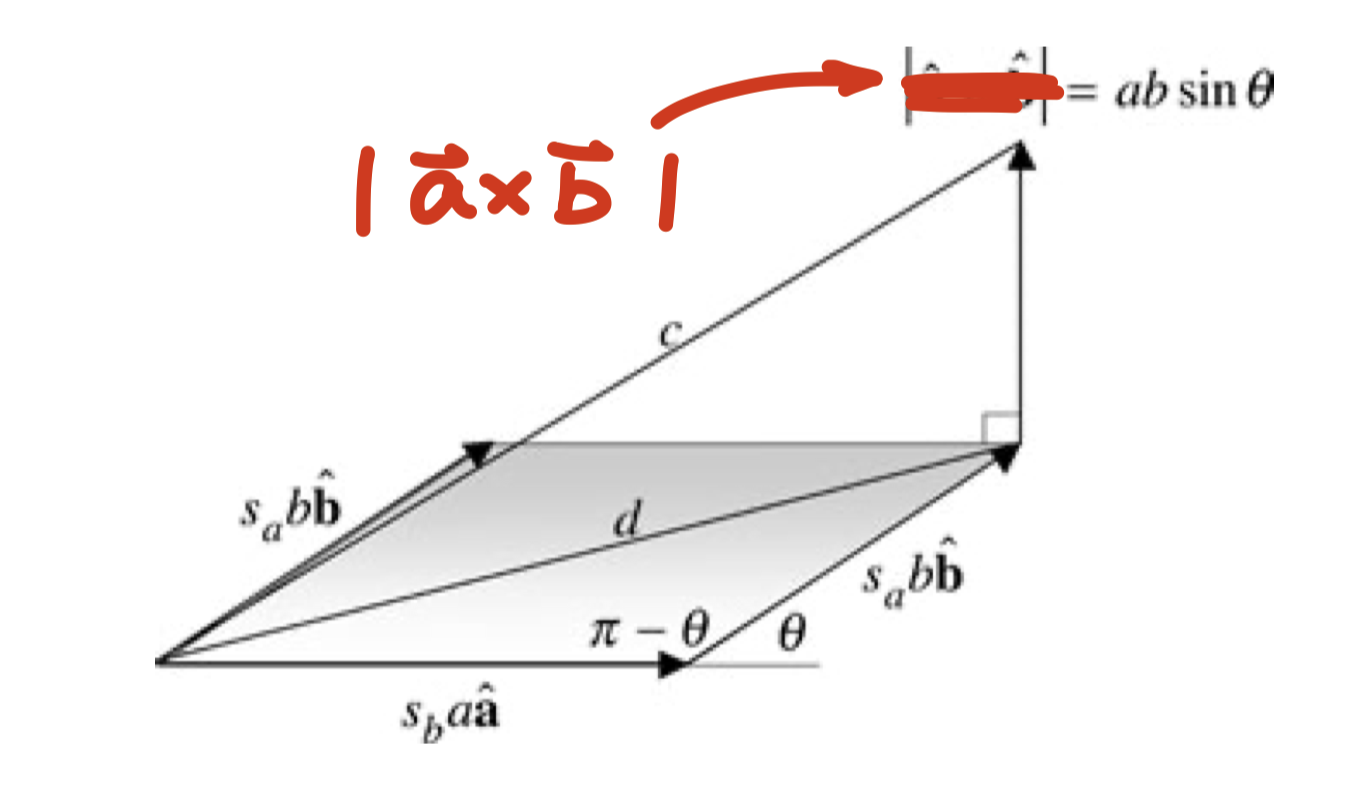
In the above picture, $\textbf{d} = s_a a \hat{\textbf{a}} + s_b b \hat{\textbf{b}}$, and the vertical vector is $\textbf{a} \times \textbf{b}$

To find $\textbf{c}^2$ we first need to find $\textbf{d}^2$:

\[\begin{aligned} \textbf{d}^2 &= \vert s_b a \hat{\textbf{a}} \vert ^2 + \vert s_a b \hat{\textbf{b}} \vert ^2 - 2 \vert s_b a \hat{\textbf{a}} \vert \vert s_a b \hat{\textbf{b}} \vert \cos (\pi - \theta) \\ &= s_b^2 a^2 + s_a^2 b^2 - 2 s_a s_b a b \cos (\pi - \theta) \\ &= s_b^2 a^2 + s_a^2 b^2 + 2 s_a s_b a b \cos \theta \end{aligned}\]

Then,

\[\begin{aligned} \textbf{c}^2 &= \textbf{d}^2 + a^2 b^2 \sin^2 \theta \\ &= s_b^2 a^2 + s_a^2 b^2 + 2 s_a s_b a b \cos \theta + a^2 b^2 \sin^2 \theta \end{aligned}\]

Remember, $\vert q_a \vert = \vert q_b \vert = 1$, so $s_a^2 + a^2 = s_b^2 + b^2 = 1$

\[\begin{aligned} \vert q_c \vert &= s_c^2 + c^2 \\ &= s_a^2 s_b^2 - 2 s_a s_b a b \cos \theta + a^2 b^2 \cos^2 \theta + s_b^2 a^2 + s_a^2 b^2 + 2 s_a s_b a b \cos \theta + a^2 b^2 \sin^2 \theta \\ &= s_a^2 s_b^2 + a^2 b^2 + s_b^2 a^2 + s_a^2 b^2 \\ &= s_a^2 (s_b^2 + b^2) + a^2 (s_b^2 + b^2) \\ &= s_a^2 + a^2 \\ &= 1 \end{aligned}\]

Square of Quaternion

\[\begin{aligned} q &= [s, \textbf{v}] \\ q^2 &= [s, \textbf{v}][s, \textbf{v}] \\ &= [s^2 - \textbf{v}^2, 2s\textbf{v} + \textbf{v} \times \textbf{v}] \\ &= [s^2 - \textbf{v}^2, 2s\textbf{v}] \end{aligned}\]

Thus, for a pure quaternion:

\[\begin{aligned} q &= [0, \textbf{v}] \\ q^2 &= [-\textbf{v}^2, 0] \end{aligned}\]

Norm of Quaternion Products

Earlier in this article I mentioned that:

\[\begin{aligned} q_a &= [s_a, \textbf{a}] \\ q_b &= [s_b, \textbf{b}] \\ q_c &= q_aq_b \\ \vert q_c \vert &= s_a^2 (s_b^2 + b^2) + a^2 (s_b^2 + b^2) \\ &= (s_a^2 + a^2)(s_b^2 + b^2) \\ &= \vert q_a \vert \vert q_b \vert \end{aligned}\]

Thus, we have:

\[\vert q_a q_b \vert = \vert q_a \vert \vert q_b \vert\]

Inverse Quaternion

By definition, inverse quaternion $q^{-1}$ satisfies $q q^{-1} = 1$

To find $q^{-1}$, we first left multiply both side by the conjugate of $q$: $q^\ast$

\[\begin{aligned} q^\ast q q^{-1} &= q^\ast \\ \vert q \vert^2 q^{-1} &= q^\ast \\ q^{-1} = \frac{q^\ast}{\vert q \vert^2} \end{aligned}\]

Note that for unit quaternion q, $q^2 = 1$, so $q^{-1} = q^\ast$

Since $(q_aq_b)^\ast = q_b^\ast q_a^\ast$, it is also true that $(q_aq_b)^{-1} = q_b^{-1} q_a^{-1}$

\[\begin{aligned} (q_aq_b)^{-1} &= \frac{(q_aq_b)^\ast}{(q_aq_b)^2} \\ &= \frac{q_b^\ast q_a^\ast}{\vert q_b \vert^2 \vert q_a \vert^2} \\ &= \frac{q_b^\ast}{\vert q_b \vert^2} \frac{q_a^\ast}{\vert q_a \vert^2} \\ &= q_b^{-1} q_a^{-1} \end{aligned}\]

Given the inverse of a quaternion, we can calculate $q_c = \frac{q_b}{q_a}$

\[\begin{aligned} q_c &= \frac{q_b}{q_a} \\ &= q_b q_a^{-1} \\ &= \frac{q_b q_a^\ast}{\vert q_a \vert^2} \end{aligned}\]

Matrix Representation of Quaternion

For quaternion multiplication, matrices can be used to represent the first quaternion.