Cross Product

I’m fucked up with cross-product. So I decided to write this shit.

Defination

The basic definition of cross-product comes from matrix determinants. Write i, j, and k in the first row and two corresponding vectors in the second and third row.

\[\begin{aligned} \textbf{a} \times \textbf{b} &= \begin{vmatrix} i & j & k \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{vmatrix} \\ &= \begin{vmatrix} a_y & a_z \\ b_y & b_z \end{vmatrix} i + \begin{vmatrix} a_x & a_z \\ b_x & b_z \end{vmatrix} j + \begin{vmatrix} a_x & a_y \\ b_x & b_y \end{vmatrix} k \\ &= (a_yb_z - a_zb_y)i + (a_xb_z - a_zb_x)j + (a_xb_y - a_yb_x)k \end{aligned}\]

From this definition, it’s obvious that order matters in the cross-product.

\[\begin{aligned} \textbf{b} \times \textbf{a} &= \begin{vmatrix} i & j & k \\ b_x & b_y & b_z \\ a_x & a_y & a_z \end{vmatrix} \\ &= \begin{vmatrix} b_y & b_z \\ a_y & a_z \end{vmatrix} i + \begin{vmatrix} b_x & b_z \\ a_x & a_z \end{vmatrix} j + \begin{vmatrix} b_x & b_y \\ a_x & a_y \end{vmatrix} k \\ &= (b_ya_z - b_za_y)i + (b_xa_z - b_za_x)j + (b_xa_y - b_ya_x)k \\ &= (a_zb_y - a_yb_z)i + (a_zb_x - a_xb_z)j + (a_yb_x - a_xb_y)k \\ &= -\textbf{a} \times \textbf{b} \end{aligned}\]

Magnitude

\[\vert \textbf{b} \times \textbf{a} \vert = \vert \textbf{a} \vert \vert \textbf{b} \vert sin\theta\]

Direction

The right-hand rule cross-product use is:

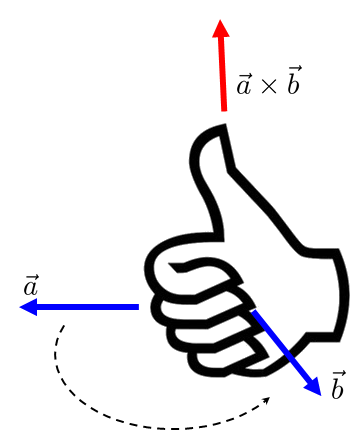
As shown in the picture, use right hand to wrap from $\textbf{a}$ to $\textbf{b}$, thumb points to the direction of $\textbf{a} \times \textbf{b}$