Complex Number Review
Complex Number Representation
Complex numbers can be represented by $\mathbb{C} = \mathbb{R} + \mathbb{I}$, where $\mathbb{R}$ is real number set and $\mathbb{I}$ is imagine number set.
Note that all complex numbers can be represented by a matrix:
\[\begin{aligned} z &= a + bi, a \in \mathbb{R} bi \in \mathbb{I} z \in \mathbb{C} \\ &= \begin{bmatrix} a & -b \\ b & a \end{bmatrix} \end{aligned}\]This matrix comes from two facts:
- Complex number $1$ can be represented by matrix: $\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$ , which is also the identity matrix.
- Complex number $i$ can be represented by matrix: $\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}$
This is because in a complex plane, both $1$ and $\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$ both keep a value intact when performing pre-multiple operation. And both $i$ and $\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}$ rotate a value 90 degrees conter-clockwise when erforming pre-multiple operation.
After we have these facts, it’s easy to see that:
\[\begin{aligned} z &= a + bi, a \in \mathbb{R} bi \in \mathbb{I} z \in \mathbb{C} \\ &= a \cdot \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} + b \cdot \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \\ &= \begin{bmatrix} a & -b \\ b & a \end{bmatrix} \end{aligned}\]Math Operation
Addition and Subtraction
\[\begin{aligned} z_1 &= a_1 + b_1i \\ z_2 &= a_2 + b_2i \\ z_1 \pm z_2 &= a_1 \pm a_2 + (b_1 \pm b_2)i \\ &= \begin{bmatrix} a_1 \pm a_2 & -(b_1 \pm b_2) \\ b_1 \pm b_2 & a_1 \pm a_2 \end{bmatrix} \end{aligned}\]For the matrix perspective here, adding two complex numbers is equivalent to adding the corresponding matrix.
Multiplication
\[\begin{aligned} z_1z_2 &= (a_1 + b_1i)(a_2 + b_2i) \\ &= (a_1a_2 - b_1b_2) + (a_1b_2 + b_1a_2)i \\ &= \begin{bmatrix} a_1a_2 - b_1b_2 & -(a_1b_2 + b_1a_2) \\ a_1b_2 + b_1a_2 & a_1a_2 - b_1b_2 \end{bmatrix} \end{aligned}\]Regular complex number multiplication is just like polynomial multiplication with $i^2 = -1$. While the matrix perspective becomes the multiplication between two matrices.
Note that the order matters when two matrices are multiplied together. However, it does not matter here. Since it turns out the result is the same no matter which matrix pre-products the other.
This makes a lot of sense since the order doesn’t matter either when it comes to complex number multiplication itself.
Square
\[\begin{aligned} z^2 &= (a + bi)^2 \\ &= (a^2 + 2abi + (bi)^2) \\ &= a^2 - b^2 + 2abi \\ &= \begin{bmatrix} a^2 - b^2 & -2ab \\ 2ab & a^2 - b^2 \end{bmatrix} \end{aligned}\]Matrix multiplication still applies here.
Norm
\[\begin{aligned} z &= a + bi \\ \vert z \vert &= \sqrt{a^2 + b^2} \\ \vert z \vert ^2 &= a^2 + b^2 \\ &= \begin{vmatrix} a & -b \\ b & a \end{vmatrix} \end{aligned}\]The regular way to get the norm of a complex number is simple: square each component and get the square root of the sum.
This led to a fact:
- The square of the norm is $a^2 + b^2$
From the matrix perspective, this is the same as the determinant of the matrix representation of the original complex number. Since the determinant of a 2x2 matrix gives:
\[\begin{vmatrix} a & b \\ c & d \end{vmatrix} = a \cdot d - b \cdot c\]Geometrically, this also makes sense. Note that for a complex number $z$, $\vert z \vert$ is the length of the vector representing that complex number in the complex plane.
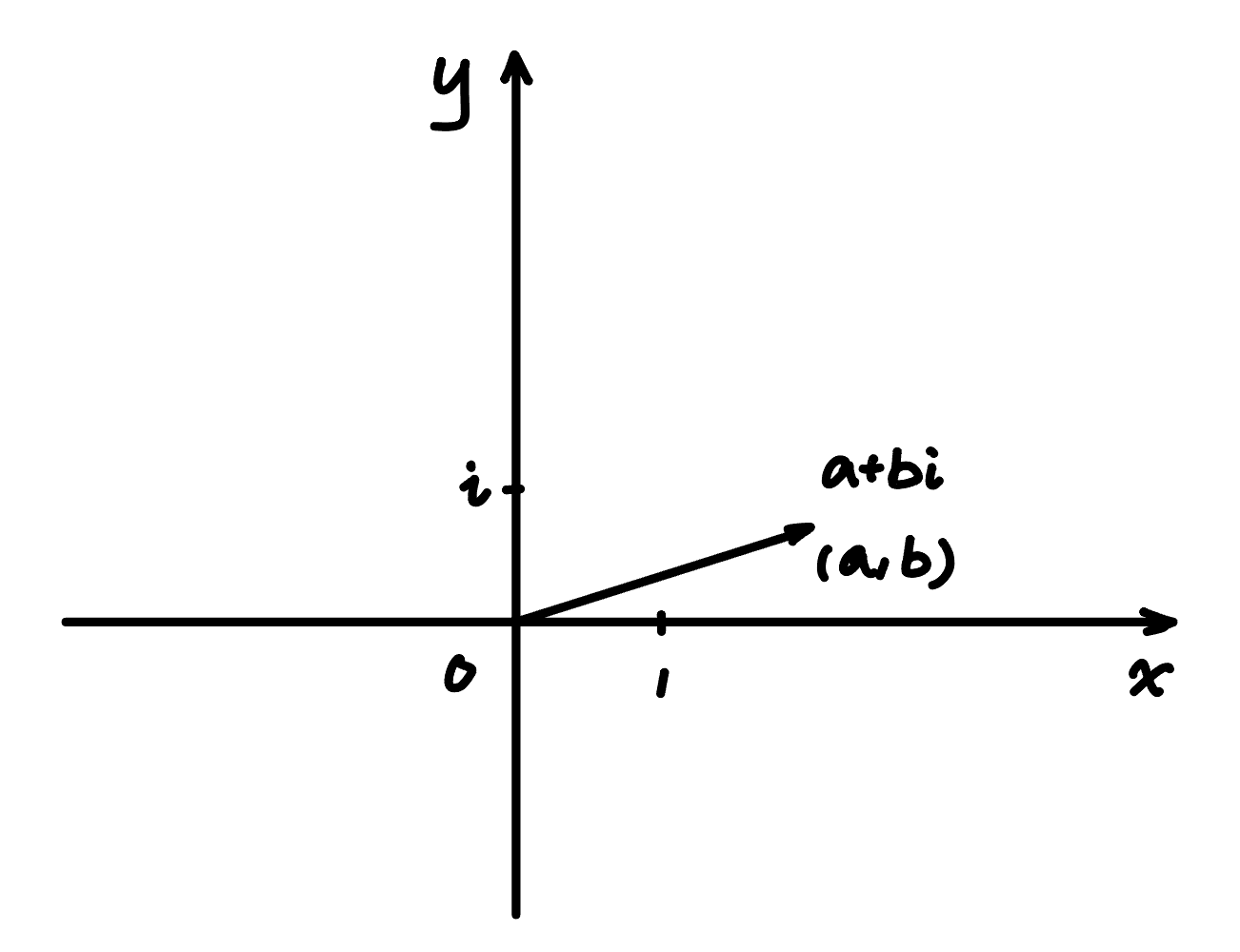
Thus, $\vert z \vert ^2$ should be the area of a square with a width of $\vert z \vert$.
Then observe the geometric definition of matrix determinant.
By defination, $\begin{vmatrix} a & b \\ c & d \end{vmatrix}$ is the area formed by $\begin{bmatrix} a \\ c \end{bmatrix}$ and $\begin{bmatrix} b \\ d \end{bmatrix}$.
Here the area is formed by $\begin{bmatrix} a \\ b \end{bmatrix}$ and $\begin{bmatrix} -b \\ a \end{bmatrix}$:
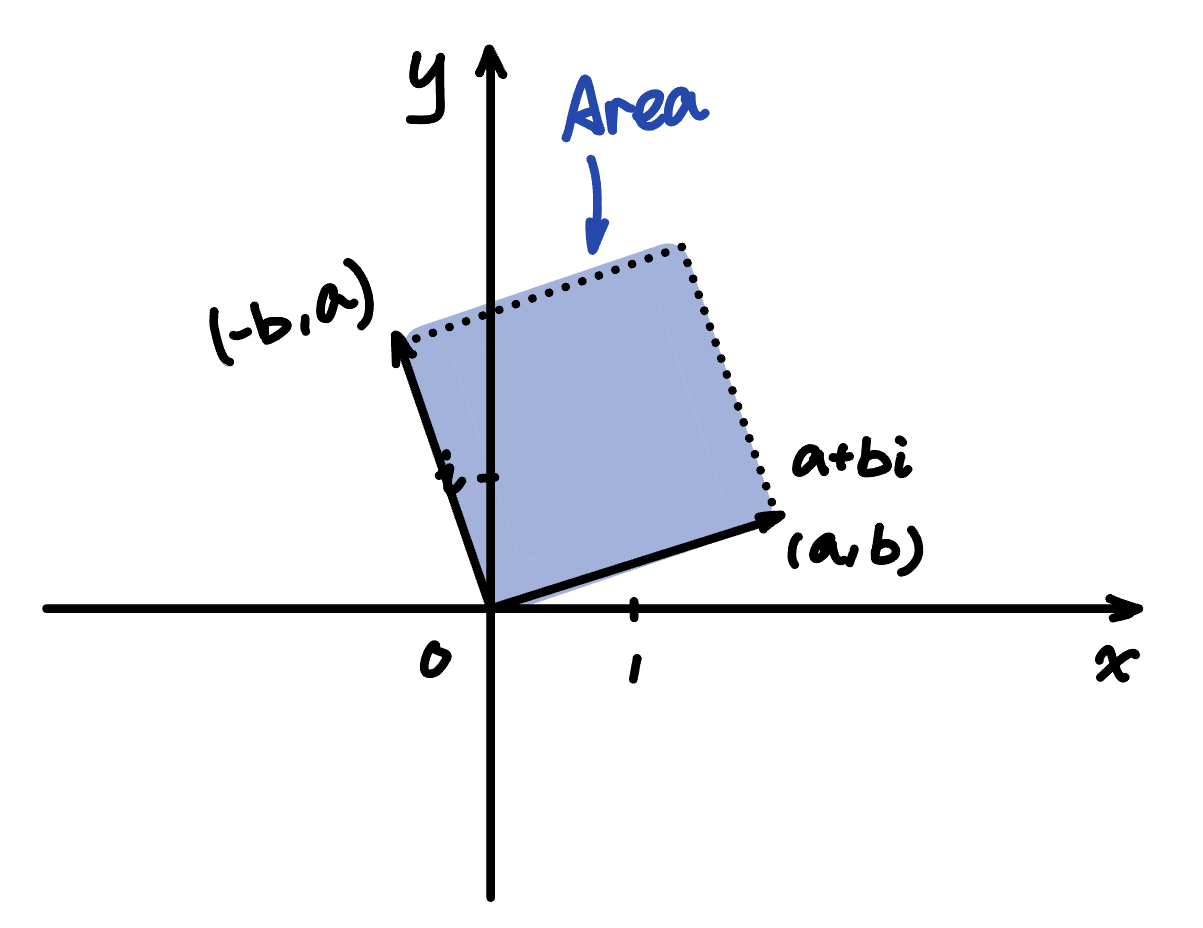
As $\begin{bmatrix} -b \\ a \end{bmatrix}$ is $\begin{bmatrix} a \\ b \end{bmatrix}$ rotated 90 degrees conter-clockwise, the final area should be what we want.
Complex Conjugate
\[\begin{aligned} z &= a + bi \\ z^* &= a - bi \\ &= \begin{bmatrix} a & b \\ -b & a \end{bmatrix} \end{aligned}\]Quotient
\[\begin{aligned} \frac{z_1}{z_2} &= \frac{a_1 + b_1i}{a_2 + b_2i} \\ &= \frac{(a_1 + b_1i)(a_2 - b_2i)}{(a_2 + b_2i)(a_2 - b_2i)} \\ &= \frac{(a_1a_2 - b_1b_2) + (a_2b_1 - a_1b_2)i}{a_2^2 + b_2^2} \\ &= z_1z_2^{-1} \\ &= \frac{1}{a_2^2 + b_2^2} \begin{bmatrix} a_1 & -b_1\\ b_1 & a_1 \end{bmatrix} \begin{bmatrix} a_2 & b_2 \\ -b_2 & a_2 \end{bmatrix}\\ &= \frac{1}{a_2^2 + b_2^2} \begin{bmatrix} a_1a_2 + b_1b_2 & a_1b_2 - b_1a_2 \\ b_1a_2 - b_1a_2 & b_1b_2 + a_1b_2 \end{bmatrix} \end{aligned}\]Here the matrix perspective becomes a little bit tricky. The overall principle is to multiply the numerator and denominator with the denominator’s conjugate. So the denominator becomes $a_2^2 + b_2^2$. Then the rest of the part becomes the simple matrix multiplication.
Inverse
\[\begin{aligned} z &= a + bi \\ \frac{1}{z} = z^{-1} &= \frac{z^*}{ \vert z \vert ^2} \\ &= \left(\frac{a}{a^2 + b^2}\right) - \left(\frac{b}{a^2 + b^2}\right)i \\ &= \frac{1}{a^2 + b^2} \begin{bmatrix} a & b \\ -b & a \end{bmatrix} \end{aligned}\]Square Root of $\pm i$
\[\begin{aligned} \sqrt{i} &= \pm \frac{\sqrt{2}}{2} (1 + i) \\ &= \pm \frac{\sqrt{2}}{2} \begin{bmatrix} 1 & -1 \\ 1 & 1 \end{bmatrix} \\ \sqrt{-i} &= \pm \frac{\sqrt{2}}{2} (1 - i) \\ &= \pm \frac{\sqrt{2}}{2} \begin{bmatrix} 1 & 1 \\ -1 & 1 \end{bmatrix} \end{aligned}\]Complex Plane
Complex Number in Complex Plane
\[\begin{aligned} z &= a + bi \\ \vert z \vert &= \sqrt{a^2 + b^2} \end{aligned}\]Polar Form
\[\begin{aligned} e^{i\theta} &= cos(\theta) + sin(\theta)i \\ z &= re^{i\theta} \\ &= r(cos(\theta) + sin(\theta)i) \\ r &= \vert z \vert \\ \theta &= arg(z) \end{aligned}\]The formula $e^{i\theta} = cos(\theta) + sin(\theta)i$ is quite complecated to remember. But a tricky way is to use derivative1.
First, start with $\theta = 0$, and $e^{i \cdot 0} = e^0 = 1$. Then take the derivative of $e^{i\theta}$: $\frac{d}{d\theta} e^{i\theta} = i \cdot e^{i\theta}$.
Since $i$ can always rotate the value 90 degrees counterclockwise, now we know that for each $\theta$, $\frac{d}{d\theta} e^{i\theta}$ is 90 degrees perpendicular to the original value.
And since $\frac{d}{d\theta} e^{i\theta}$ represents the rate of change of $e^{i\theta}$, so it can be known that $e^{i\theta}$ falls on a circle certer at (0, 0), and have radius of 1, rotating counterclockwise with speed of 1.
When $\theta = \frac{\pi}{2}$, the vector rotate path length should be $\frac{\pi}{2}$. So the $e^{i * \frac{\pi}{2}} = i$ which is also (0, 1).
Note that $\vert e^{i \theta} \vert = 1$ since it falls on the unit circle.
For a general polar form vector, we need both $r$ and $\theta$.
Product
\[\begin{aligned} z &= re^{i\theta} \\ w &= se^{i\phi} \\ zw &= rse^{(\theta + \phi)i} \\ &= rs(cos(\theta + \phi) + sin(\theta + \phi)i) \end{aligned}\]The polar form complex number production obeys basic exponential multiplication rules. But it also shows the fact that when two complex number are multiplied, their magnitude get multiplied and angle are added.
Quotient
\[\begin{aligned} \frac{z}{w} &= \frac{r}{s}e^{\theta - \phi} \\ &= \frac{r}{s}(cos(\theta - \phi) + sin(\theta - \phi)i) \end{aligned}\]Rotors
\[\begin{aligned} \boldsymbol{R}_\theta &= cos(\theta) + sin(\theta)i \\ \boldsymbol{R}_\theta^{\div} &= cos(\theta) - sin(\theta)i \end{aligned}\]The product and quotient rules lead to the idea of rotors. While a complex number with a magnitude of 1 will not change the magnitude of the target vector. But the angle is presumed as the rotated angle.