Terminal Velocity

Terminal Velocity Problem

Considering free falling with air resistance. The force of air resistance can be modeled by $-kv$, where $k$ is a constant and $v$ is the velocity.

The gravity applied on the object can be modeled as $-mg$.

Thus, the net force $F = -mg - kv$. Not that v is negative when the mass is falling.

\[\begin{aligned} m \frac{dv}{dt} &= -mg - kv \\ \frac{dv}{dt} + \frac{k}{m} v &= -m \\ p(t) = \frac{k}{m} ,& \quad g(t) = -m \\ \end{aligned}\]

Next, we need to solve this linear differential equation.

\[\mu (t) = e^{\int_{0}^{t} \frac{k}{m} dt} = e^{kt/m}\]

Thus,

\[\begin{aligned} v (t) &= e^{-kt/m} \int_{0}^{t} e^{kt/m} (-g) dt \\ \int_{0}^{t} e^{kt/m} (-g) dt &= (- \frac{mg}{k} e^{kt/m}) \vert_{0}^{t} \\ v (t) &= e^{-kt/m} (- \frac{mg}{k} e^{kt/m}) \vert_{0}^{t} \\ &= e^{-kt/m} (-\frac{mg}{k} e^{kt/m} + \frac{mg}{k}) \\ &= - \frac{mg}{k} (1 - e^{-kt/m}) \end{aligned}\]

This equation describes the velocity of the mass at arbitrary time t. Notice that when $t \to \infty$, $(1 - e^{-kt/m}) \to 1$, and $v \to -\frac{mg}{k}$, which is the terminal velocity.

Example

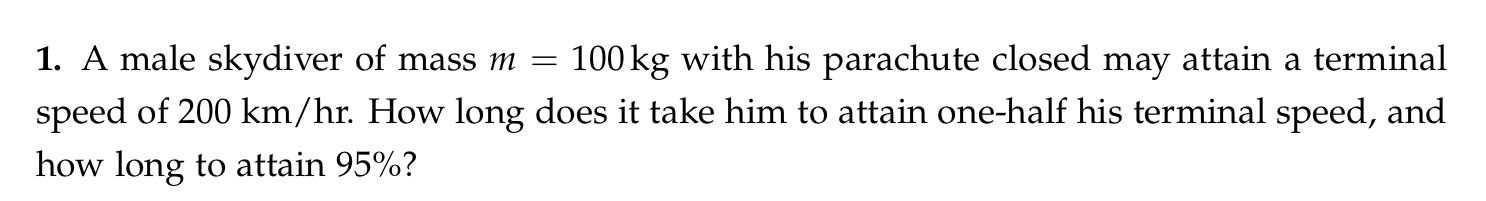
Given the terminal velocity:

\[v_{\infty} = -200 km/h = -\frac{500}{9} m/s\]

Calculate k by:

\[\begin{aligned} k &= - \frac{mg}{v_{\infty}} = \frac{441}{25} \\ \end{aligned}\]

To attain one-half the speed at $t_1$

\[\begin{aligned} v(t_1) &= \frac{1}{2} v_{\infty} \\ 1 - e^{-kt_1/m} &= 0.5 \\ e^{-kt_1/m} &= 0.5 \\ t_1 &= - \frac{m}{k} ln(0.5) \\ t_1 &= 3.92s \end{aligned}\]

To attain 95% of the speed at $t_2$

\[\begin{aligned} t_2 &= - \frac{m}{k} ln(0.05) \\ &= 16.98 \end{aligned}\]