Logistic Map
Definition
\[x_{n+1} = f(x_n)\]Start from $x_0$
Fixed Point
Logistic maps can have fixed points $x_\ast$. For fixed points, $x_\ast = f(x_\ast)$.
The fixed point can be stable or unstable.
Start by choosing $x_0$ near the fixed point; if the fixed point is stable, $x$ will converge to the fixed point. If the fixed point is unstable, $x$ will move away from the fixed point.
The method to analyze if a fixed point is stable or unstable is called linear stability analysis.
Linear Stability Analysis
Start by letting
\[\begin{aligned} x_n &= x_\ast + \epsilon_n \\ x_{n+1} &= x_\ast + \epsilon_{n+1} \end{aligned}\]If $\epsilon_{n+1}$ is larger than $\epsilon_n$, the fixed point is unstable.
\[\begin{aligned} x_\ast + \epsilon_{n+1} &= f(x_\ast + \epsilon_n) \end{aligned}\]Expand $f(x_\ast + \epsilon_n)$ with Taylor series will give us:
\[\begin{aligned} f(x_\ast + \epsilon_n) &= f(x_\ast) + \epsilon_n f'(x_\ast) + \frac{\epsilon_n^2}{2!} f''(x_\ast) + \cdots \end{aligned}\]When analyzing with numerical methods, drop the none linear terms:
\[\begin{aligned} f(x_\ast + \epsilon_n) &= f(x_\ast) + \epsilon_n f'(x_\ast) + \frac{\epsilon_n^2}{2!} f''(x_\ast) + \cdots \\ &\approx f(x_\ast) + \epsilon_n f'(x_\ast) \end{aligned}\]Given $x_\ast = f(x_\ast)$,
\[\begin{aligned} x_\ast + \epsilon_{n+1} &= f(x_\ast) + \epsilon_n f'(x_\ast) \\ \epsilon_{n+1} &= \epsilon_n f'(x_\ast) \\ \frac{\epsilon_{n+1}}{\epsilon_n} &= f'(x_\ast) \end{aligned}\]Since $x_\ast$ is stable when $\vert \frac{\epsilon_{n+1}}{\epsilon_n} \vert$ is less than one, $x_\ast$ is stable when $\vert f’(x_\ast) \vert < 1$
Otherwise, if $\vert f’(x_\ast) \vert > 1$, $x_\ast$ is unstable.
Example
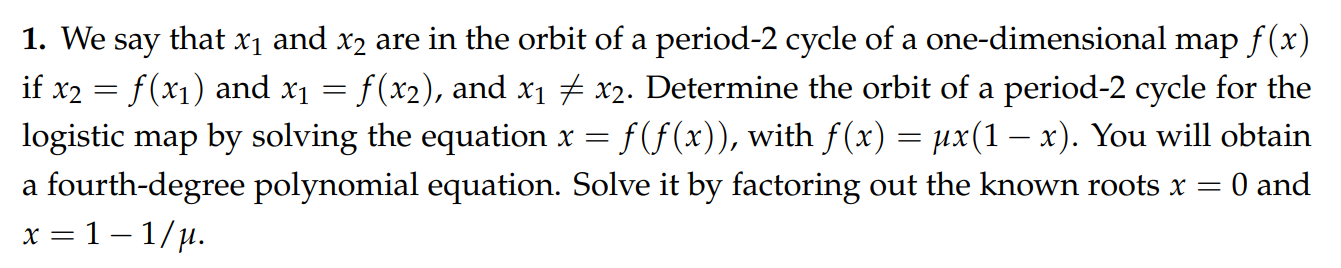
By definition, $x_\ast = f(x_\ast)$
\[\begin{aligned} %% Expand the function. x = f(f(x)) &= \mu (\mu x (1-x)) \ast (1 - \mu x(1 - x)) \\ &= (\mu^2 x - \mu^2 x^2) \cdot (1 - \mu x + \mu x^2) \\ \mu^3 x^4 - 2 \mu^3 x^3 + \mu^2 (\mu + 1) x^2 + (1 - \mu^2) x &= 0 \end{aligned}\]Given the two solutions $x=0$ and $x = 1 - \frac{1}{\mu}$,
First factor out $x$:
\[\begin{aligned} \mu^3 x^3 - 2 \mu^3 x^2 + \mu^2(\mu + 1)x + (1 - \mu^2) = 0 \end{aligned}\]Further factor out $(x - (1 - \frac{1}{\mu}))$:
\[\begin{aligned} \mu^3 x^3 - 2 \mu^3 x^2 + \mu^2(\mu + 1)x + (1 - \mu^2) &= 0 \\ \mu^3 x^2 - (\mu^3 + \mu^2)x + (\mu^2 + \mu) &= 0 \end{aligned}\]We can further factor out $\mu$:
\[\begin{aligned} \mu^2 x^2 - \mu (\mu + 1)x + (\mu + 1) &= 0 \end{aligned}\]Solve for x:
\[x = \frac{1}{2 \mu} ((\mu + 1) \pm \sqrt{(\mu + 1)(\mu - 3)})\]